ZENONE DI ELEA 14 Gennaio 2022 – Posted in: Biografie, Lo Sapevi che – Tags: #aneddotimatematici #zenonedielea #ippaso #fenomenologiadellamatematica #fenomenologia #biografie, #paradossi #paradossodellostadio #paradossodellatartaruga #paradossodiachille #paradossodellafreccia #freccia
Continuando il nostro viaggio tra i matematici dell’antichità incontriamo Zenone di Elea (489 – 431 a.C.) .
E’stato un filosofo greco della Magna Grecia (Campania), membro della scuola eleatica fondata da Parmenide, della sua vita si sa ben poco se non le informazioni biografiche che possono ricavarsi dal dialogo “Parmenide” di Platone. Zenone soffermò la sua attenzione su molti fenomeni fisici ricavandone più di quaranta Paradossi, intesi questi come contraddizione logica contenuta nella stessa argomentazione. Aristotele lo definisce inventore della dialettica. È conosciuto soprattutto per i suoi paradossi, che Bertrand Russell definì come «smisuratamente sottili e profondi»
I più noti sono tre e riguardano sempre l’impossibilità del moto: il “paradosso dello stadio”, “Achille e la tartaruga” e il “paradosso della freccia”. In tutti egli voleva dimostrare che accettare la presenza di movimento nella realtà porta a delle contraddizioni. Questi concetti hanno avuto attenzione dei matematici per secoli perché implicano il concetto di infinita divisibilità dello spazio e per secoli, incredibilmente, sono rimasti irrisolti.
Paradosso dello stadio
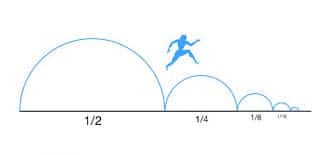
Questo paradosso afferma che non è possibile arrivare alla fine di uno stadio (dove per stadio egli intendeva un’unità di misura di lunghezza pari a 600 piedi ossia 182,88 metri), infatti bisognerebbe dapprima giungere a metà tragitto, poi si dovrebbe raggiungere la metà della metà, successivamente la metà della metà della metà, e così via fino all’infinito. Una infinità di metà separa il punto di partenza da quello di arrivo. Si tratta allora di percorrere in un tempo finito tratti infiniti, il che è impossibile, dunque il movimento non è reale. L’errore di Zenone, è che considera gli intervalli sempre finiti; ma questo non è proprio preciso. Gli intervalli sono sì finiti, ma la loro lunghezza tende a zero, ovvero diventano infinitesimi. Per stranezze matematiche che però vengono evidenziate nelle serie numeriche, non è detto che la somma di infiniti termini finiti dia sempre un termine infinito.
zenone
Paradosso di Achille e la tartaruga
Zenone riteneva che due corpi qualsiasi che sono in movimento nella stessa direzione, anche se il primo più veloce del secondo, non si possono mai incontrare. Per dimostrare questa sua affermazione immaginò di dover confrontare il “piè veloce” Achille con la tartaruga, notoriamente lenta. Achille doveva affrontare una gara di velocità ad handicap, cioè con piccolo svantaggio, con una tartaruga. Achille doveva partire da un punto A e la tartaruga aveva un vantaggio iniziale partendo da un punto B. Achille, pur muovendosi con velocità evidentemente maggiore della tartaruga non l’avrebbe mai raggiunta. Infatti supponendo che il segmento AB fosse il vantaggio della tartaruga su Achille, quest’ultimo sarebbe dovuto arrivare in B per raggiungerla ma nel frattempo la tartaruga si sarebbe spostata in C e mentre Achille sarebbe arrivato in C la tartaruga sarebbe passata in D e così via…per spazi infinitamente più piccoli senza mai raggiungerla.
Anche in questo caso c’era un errore simile nel ragionamento di Zenone: egli supponeva implicitamente che la somma infinita di lunghezze finite, per quanto piccole, desse sempre un risultato infinito. Questa ipotesi sembra accettabile intuitivamente è matematicamente sbagliata e si può comprendere con lo studio delle serie convergenti che si studiano in analisi matematica.

zenone
Paradosso della freccia
Con questo paradosso Zenone voleva dimostrare che il movimento non esiste prendendo come esempio un corpo in movimento. Considerando una freccia lanciata nello spazio essa era in realtà ferma perché in ogni istante in cui la freccia era in volo essa avrebbe occupato uno spazio uguale alla propria lunghezza e poiché ciò che occupa uno spazio identico è in riposo la freccia sarebbe stata ferma in tutti gli istanti del suo moto. I matematici riuscirono a confutare questo paradosso soltanto alla fine del diciannovesimo secolo quando fu sviluppata la teoria dei numeri reali.
zenone
A proposito di quest’ultimo paradosso, si narra che il filosofo Antistene “il cinico”, che non aveva molto in simpatia Zenone proprio a causa dei suoi paradossi, andò a trovarlo per discutere delle sue strambe teorie. Però, non riuscendo a controbattere Zenone sul paradosso della freccia, cominciò a camminare nervosamente su e giù, tanto che Zenone, innervositosi, esclamò: – Ma vuoi stare fermo un momento! – Ah! Allora ammetti che mi muovo? – rispose Antistene.
Per oltre due millenni i paradossi di Zenone sono stati discussi ed analizzati, ma solo oggi, grazie a una formulazione dell’analisi matematica, sviluppata nell’ultimo decennio, è possibile risolverli. Per molti secoli la logica di Zenone è rimasta pressoché intatta, e ciò dimostra la tenacia dei suoi argomenti.
Aneddoti su Zenone di Elea:
1) congiurò contro Demilo (o Nearco, secondo Diodoro) tiranno della città, ma fu catturato e sottoposto a tortura. Narra lo storico Plutarco che il filosofo, per non tradire gli altri congiurati, con un morso si recise la lingua e la scagliò sprezzante verso il despota.
2) Narra lo storico Diodoro Siculo che Zenone congiurò contro Nearco, ma fu scoperto e sottoposto a tortura per fargli svelare il nome dei suoi complici. Scoperto e interrogato da Nearco, pur tormentato, resistette, e ad un certo punto, fingendo di essere in punto di morte, gridò: – Fermatevi! Dirò tutta la verità.
Sospesa la tortura, Zenone chiese a Nearco di avvicinarsi perché voleva dirgli nell’orecchio tutto ciò che sapeva. Il tiranno accostò l’orecchio alla bocca di Zenone che subito glielo afferrò con i denti e non lo mollò fino a che i servi del tiranno lo trafissero provocandogli la morte.
© copyright 2022 – tutti i diritti sono riservati.