TEODORO DI CIRENE 27 Gennaio 2022 – Posted in: Lo Sapevi che – Tags: #fenomenologiadellalingua #matematica #spirale #teodoro #teodorodicirene #profMelissa #antichità
Continuiamo il nostro viaggio alla scoperta dei matematici dell’antichità.
Uno dei più grandi matematici fu Teodoro di Cirene che fu considerato uno studioso di geometria di grande impatto sulla matematica dai suoi contemporanei. Nacque a Cirene, nel nord Africa il 465 a,C. e fu contemporaneo di Ippocrate di Chio, quindi visse nel IV sec.a.C. Morì sempre a Cirene nel 398a.C. Sebbene nessuno dei suoi lavori sia giunto fino a noi è noto che Teodoro si interessò di geometria ma anche dei numeri irrazionali, cioè numeri non esprimibili come rapporto di due numeri interi. Fedele pitagorico, fu filosofo della scuola di Cirene. Pensava che il piacere e il dolore non corrispondessero né al Bene né al Male e che per essere felici bastava saper essere “saggio”. Si interessò anche di astronomia e musica. Si dice che egli sia stato uno studente di Protagora e nel Teeteto, dialogo di Platone, si narra che egli stesso insegnò matematica a Platone, forse anche a Socrate, ad Atene. Infatti nel dialogo si racconta che quando Platone si recò a Cirene incontrò Teodoro che gli insegnò i numeri irrazionali.
Molti aspetti della sua vita, inclusi l’esatta data di nascita e di morte sono sconosciuti. Secondo numerosi studiosi antichi come Senofonte, Diogene Laerzio, Platone e Proclo il maggior contributo dato da Teodoro alla matematica fu la prova che le radici quadrate dei numeri dal 3 al 17 (tranne ovviamente 4, 9 e 16) sono numeri irrazionali. Non è noto come sia stato capace di provarlo ma si suppone lo abbia fatto per via geometrica.
LA SUA OPERA PIÙ’ NOTA
La sua opera più nota è la costruzione della cosiddetta Spirale di Teodoro, una spirale composta da triangoli rettangoli posti fianco a fianco che ora porta il suo nome. Nei tempi moderni numerosi matematici hanno riprodotto con successo le conclusioni di Teodoro sui numeri irrazionali. Vediamo quale è il procedimento per costruire la famosa spirale. SI costruisce un triangolo rettangolo isoscele di cateti uguali ad 1. L’ipotenusa, per il teorema di Pitagora misura allora radice di 2. Si costruisce poi sull’ipotenusa che misura radice di 2, il triangolo rettangolo che ha come cateto maggiore questo lato e il cateto minore che misura sempre 1. L’ipotenusa di questo secondo triangolo rettangolo misurerà radice di 3; se si continua con questa costruzione di triangoli rettangoli si potrebbe costruire la radice quadrata di qualsiasi numero esistente e questo è l’unico metodo geometrico che permette di costruire la radice quadrata di un qualsiasi numero. I triangoli nella spirale non si sovrappongono se si disegna fino a quello avente ipotenusa che misura radice di 17.
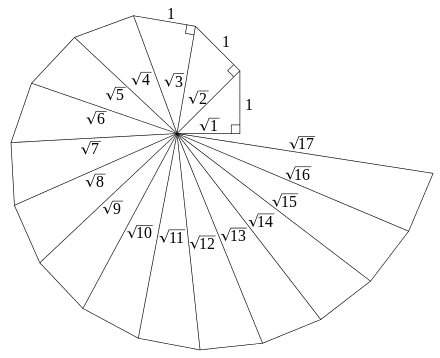
La Spirale di Teodoro di Cirene
Nota storica
Attenti a non confondere!
Con il nome Teodoro di Cirene vengono indicati:
- Teodoro di Cirene (morto nel 310) – vescovo e santo martire, celebrato il 4 luglio
- Teodoro di Cirene (IV-III secolo a.C.) – detto “l’ateo”, esponente della Scuola cirenaica
- Teodoro di Cirene (V secolo a.C.) – matematico della Scuola pitagorica
© copyright 2022 – tutti i diritti sono riservati.
