IPPOCRATE DI CHIO 25 Gennaio 2022 – Posted in: Lo Sapevi che – Tags: #aneddotimatematici #ippocrate #chio #fenomenologiadellamatematica #fenomenologia #biografie, #lunule, #profMelissa
Continuando il nostro viaggio tra i matematici dell’antichità incontriamo Ippocrate di Chio, nato ad Atene tra il 450 e il 420 a.C., allievo di Enopide a Chio.
Fu membro della scuola pitagorica dalla quale fu espulso perché pare vendesse conoscenze geometriche in cambio di denaro. Successivamente, come narra Aristotele, fu egli stesso vittima di una truffa e perse tutti i suoi averi dai doganieri di Bisanzio. Per questo motivo decise, per guadagnarsi da vivere, di darsi all’insegnamento della geometria fermandosi ad Atene fondando la scuola geometrica ateniese.
A CHE COSA E’ DOVUTA LA SUA FAMA?
La sua fama è dovuta al fatto che si occupò per primo di due problemi famosissimi nella geometria greca: la quadratura del cerchio e la duplicazione del cubo.
Ippocrate fu l’inventore delle dimostrazioni per assurdo cioè quelle che partono dalla negazione della tesi di un teorema dimostrando che quest’ultima conduce ad una contraddizione logica e quindi se la tesi non può essere falsa deve necessariamente essere vera.
Ippocrate fu il primo a tentare di unire tutte le catene deduttive della geometria in un unico sistema capace di contenere una vasta gamma di conoscenze geometriche elementari; scrisse, infatti, un libro intitolato ELEMENTI verso la fine del V sec.a.C.
A lui è dovuto il primo tentativo di esposizione sistematica della geometria, secondo Proclo, fu il primo autore di un libro di Elementi, e ciò circa un secolo e mezzo prima di Euclide.
LA QUADRATURA DELLE LUNULE
Gli Elementi di Ippocrate sono andati perduti, ma sul loro autore esiste una documentazione importante in un frammento che il filosofo bizantino Simplicio (VI sec. d.C.) dichiara di aver copiato integralmente dalla Storia della geometria di Eudemo. Questo frammento tratta della quadratura delle lunule.
Egli riuscì a calcolare l’area di una lunula senza conoscere l’area del cerchio (per la quale bisogna attendere ancora quasi due secoli con Archimede) ma soltanto con il teorema di Pitagora.
Disegniamo la Fig. 1, in cui si vede molto bene cosa è una lunula. Il nome stesso lo fa capire: una falce di luna, in particolare quella azzurra.
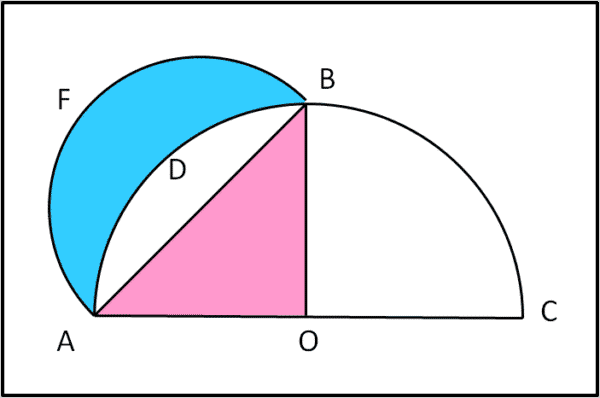
Ippocrate – Figura 1
La sua costruzione è semplice. Traccio la semicirconferenza di diametro AC, sia OB il raggio perpendicolare al diametro AC. Congiungo A con B e traccio la semicirconferenza di diametro AB. Quella in azzurro è una lunula di cui voglio calcolare l’area. Ippocrate non conosceva come si calcola l’area del cerchio ma sapeva solo che quest’ultima era proporzionale al quadrato del diametro. Applicando questa proprietà ed il teorema di Pitagora egli riuscì a dimostrare che l’area della lunula è uguale all’area del triangolo rettangolo isoscele AOB (che in questa figura è colorato di rosa) la cui ipotenusa coincide con il diametro AB. Ovviamente la dimostrazione è stata omessa per semplicità.
No, Ippocrate non ha ottenuto la quadratura del cerchio… ma ha ottenuto la quadratura delle … lunule, infatti la somma delle aree di 4 lunule è uguale all’area del quadrato di lato uguale all’ampiezza delle lunule, come mostrato in Fig. 2.
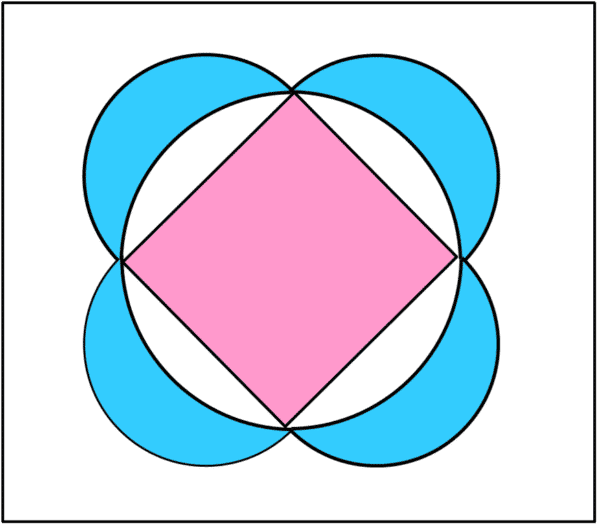
Ippocrate – Figura 2
Vi piace questo viaggio tra i matematici dell’antichità? Ne consigliate altri? Attendo nei commenti vostri preziosi spunti, grazie!
© copyright 2022 – tutti i diritti sono riservati.
