STABILISCI I VALORI 23 Novembre 2021 – Posted in: Momento Ludus – Tags: #fenomenologiadellamatematica, #indovinellomatematico #momentoludus #divertimento #fenomenologia, #profMelissa
Indovinelli matematici : STABILISCI I VALORI…!
La disciplina della matematica è una delle più difficili in assoluto. Una disciplina “ostica” non per tutti, una materia che con il corso degli anni si è evoluta, sempre di più diventando a detta di molti sempre più difficile. Come renderla più gradevole e meno frenante? Divertendo! Sono così nati gli indovinelli matematici, una vera risorsa per avvicinarsi alla materia.
Ovviamente senza applicazione e studio si fa poca strada ma esistono molti metodi che vi permettono di impararla come si deve.Avete mai sentito parlare fino ad oggi di indovinelli matematici? Siamo sicuri di sì. Proseguendo nel nostro articolo, cominceremo con la collaborazione della Prof.ssa Melissa che da anni insegna in ogni ambito didattico e assume proprio come cavallo di battaglia, come chiave di apprendimento della materia, il metodo “divertente” e pratico. Con lei vedremo una lista dettagliata dei migliori enigmi da risolvere utilizzando le proprie basi. Capacità di logica e di matematica, dal più semplice al più complicato in assoluto, alcuni con dei trabocchetti a cui stare molto attenti.
Ad ogni modo, sono tutti con soluzioni e spiegazione finale dettagliata, in modo da aiutarvi a capire come mai la soluzione sia quella.
Un’utile palestra per poter allenare nel miglior modo possibile la propria abilità. Un buon metodo per tenere in allenamento la mente cosi da applicarvi il più possibile in una materia difficile come la matematica.
Forza cominciamo ad allenarci!
8° INDOVINELLO MATEMATICO/LOGICO DELLA PROF.SSA MELISSA
Stabilisci i valori interi di A, B, C e D che soddisfano le seguenti richieste:
A + B = 14
: x
C – D = -2
= =
4 24
SOLUZIONE
A=8, B=6, C=2 e D=4
Infatti
8+6=14
2-4=-2
8:2=4
6×4=24
Per risolvere questa tabella devi trovare le soluzioni del seguente sistema:
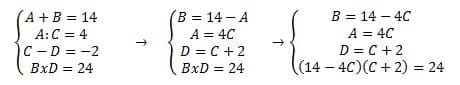
valori
L’ultima equazione contiene solo la C come incognita e diventa un’equazione di secondo grado completa:
2 C ² – 3 C-2=0
Le cui soluzioni sono C=2 e C=1/2
Poiché il problema richiede solo le soluzioni intere si accetta soltanto il valore C=2 e da questo si ricavano tutti gli altri valori.
© copyright 2021 – tutti i diritti sono riservati.
