IPPASO DI METAPONTO 12 Gennaio 2022 – Posted in: Lo Sapevi che – Tags: #aneddotimatematici #ippasodimetaponto #ippaso #fenomenologiadellamatematica #fenomenologia #biografie, #fenomenologiadellamatematica, #matematica, #profMelissa
Ippaso di Metaponto (VI-V sec. A.C.)
Continuando il nostro viaggio tra i matematici dell’antichità incontriamo Ippaso di Metaponto (MT). Egli visse tra il VI e il V secolo a.C. ed è oggi considerato la personalità più rilevante della scuola pitagorica antica.
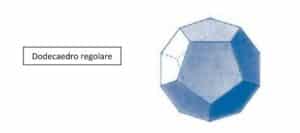
A lui è attribuita la descrizione del dodecaedro regolare e la dimostrazione della sua “inscrivibilità” nella sfera.
I pitagorici erano profondamente impegnati nella cosmologia e nella geometria, erano anche investiti nel misticismo numerologico: la visione che la realtà è, al livello più fondamentale, matematica, ed erano convinti che i numeri particolari rappresentavano certi aspetti della realtà: 1 era l’origine di tutte le cose, 2 rappresentava la materia, 4 il matrimonio, 10 la perfezione. Il cosmo pitagorico mostrava un ordine e un’armonia profondi, insieme matematici e musicali. Il mondo visibile, in particolare i movimenti dei cieli, rifletteva le relazioni armoniose tra i numeri che formavano la base della realtà, relazioni che i matematici oggi chiamerebbero rapporti – la traduzione latina da cui deriva il nostro termine moderno di “razionalità”.
Ma Ippaso fu un discepolo indisciplinato tanto da avere il coraggio di contraddire il maestro. La fatidica scoperta di Ippaso fu che una realtà fondamentalmente matematica potrebbe non essere così razionale, dopotutto. Studiando la geometria dei triangoli rettangoli isosceli, Ippaso scoprì l’esistenza di quelli che oggi chiamiamo “numeri irrazionali” –(non perché abbiano un difetto psicologico) –ad esempio il numero √2= 1, 41421 35623 73095 04880 16887 24209 69807 85696 71875 37694…ad esempio scritto con le prime cinquanta cifre decimali, numeri che hanno infinite cifre decimali che non si ripetono mai con la stessa sequenza, numeri che soprattutto non possono essere espressi come rapporto tra due numeri interi. Sorprendentemente la scoperta avvenne studiando un triangolo rettangolo, il più semplice possibile: quello con i due cateti di lunghezza uguale a valore uno, un triangolo rettangolo isoscele. In effetti, in quel triangolo l’ipotenusa, per il teorema di Pitagora, era uguale alla radice di due. Quest’…ultima però non si può esprimere come un numero razionale positivo! L’esistenza di tali numeri confuta l’idea che l’universo abbia la natura di un rapporto matematico: se i numeri possono essere essi stessi irrazionali, allora anche il fondamento stesso del cosmo è irrazionale, e l’intera concezione pitagorica del mondo crolla. Il segreto non poteva essere rivelato. Se l’universo pitagorico magnificamente razionale doveva sopravvivere, Ippaso doveva morire.
A questo punto Ippaso, per il suo tradimento, fu messo al bando dai pitagorici che, si racconta, gli innalzarono un monumento funebre, perché fosse chiaro che per loro era morto. Secondo il filosofo greco Proclo (412-483 d.C.) Ippaso perì nei pressi di Crotone in un naufragio procuratogli da Giove adirato contro di lui.
“Se l’uomo non sapesse di matematica non si eleverebbe di un sol palmo da terra.” (Galileo Galilei)
© copyright 2022 – tutti i diritti sono riservati.